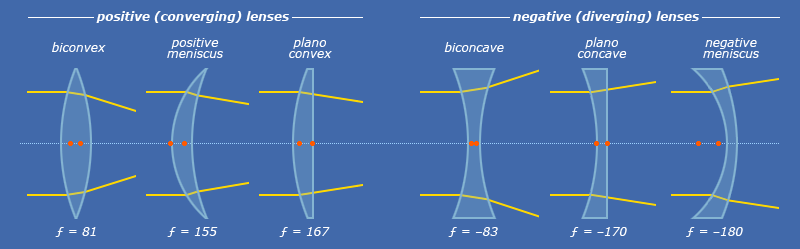
It is not rigorous to judge the positive and negative focal length of the lens simply by looking. If you have to “look”, judge by observing whether the thickness of the center of the lens is greater than the thickness of the edge. The lens with the thickness of the center greater than the thickness of the edge is generally positive. Generally, the lenticular lens is positive, the lenticular lens is negative, and the meniscus lens can be positive or negative (the above judgment is based on experience and is not very accurate).
The focal length of lens is determined by its thickness, refractive index and curvature, which is a complex formula [1]:
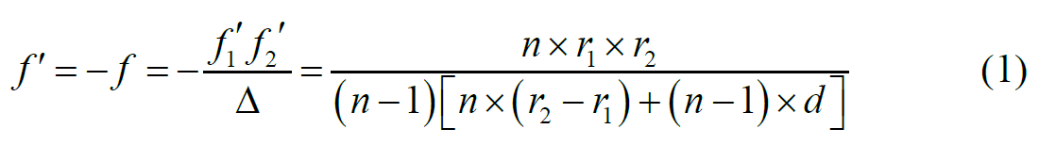
In Formula 1, R1 and R2 are the radius of curvature of the front and rear surfaces of the lens respectively, D is the thickness of the lens, and N is the refractive index of the lens material.
Based on Equation 1, the positive and negative focal lengths of various types of lenses are briefly discussed [2]:
1. Biconvex lens
For this type of lens, R1 > 0, R2 < 0. It can be seen from equation 1 that if the two surfaces R1 and R2 of the lens are kept unchanged, the focal length can be positive or negative with the different thickness D.
2. Double concave lens
For this type of lens, R1 < 0, R2 > 0. It can be seen from equation 1 that the focal length is always negative.
3. Plane convex lens
It is assumed that the front surface of the lens R1 > 0, R2 = ∞. From equation 1, the lens focal length formula is simplified to
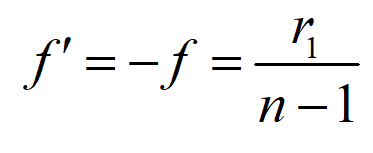
Therefore, the image square focal length of the plano convex lens is always positive, and its focal length is independent of the lens thickness.
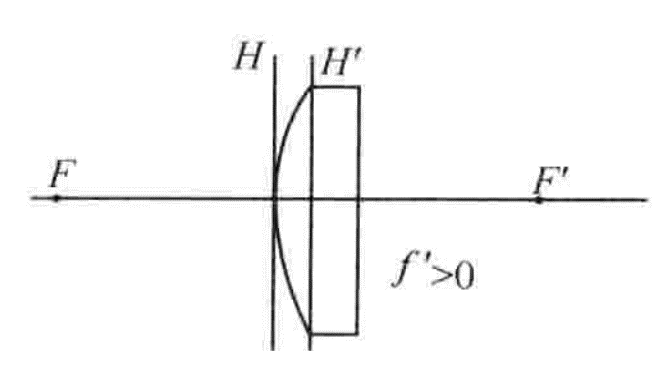
4. Plane concave lens
Assuming that the front surface of the lens is concave, R1 < 0, R2 = ∞, its focal length is always negative, and its focal length is independent of the lens thickness.
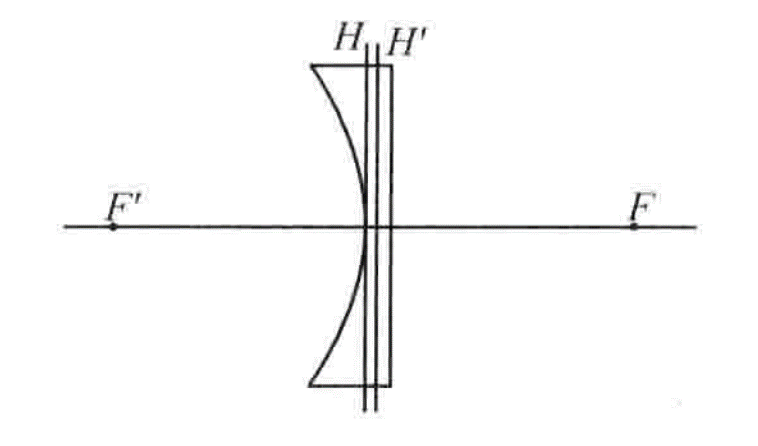
5. Meniscus convex lens
For this type of lens, the symbols of the radius of curvature of the two surfaces are the same, but the absolute value of the radius of curvature of the convex surface is smaller. It can be seen from equation 1 that the focal length is always positive.
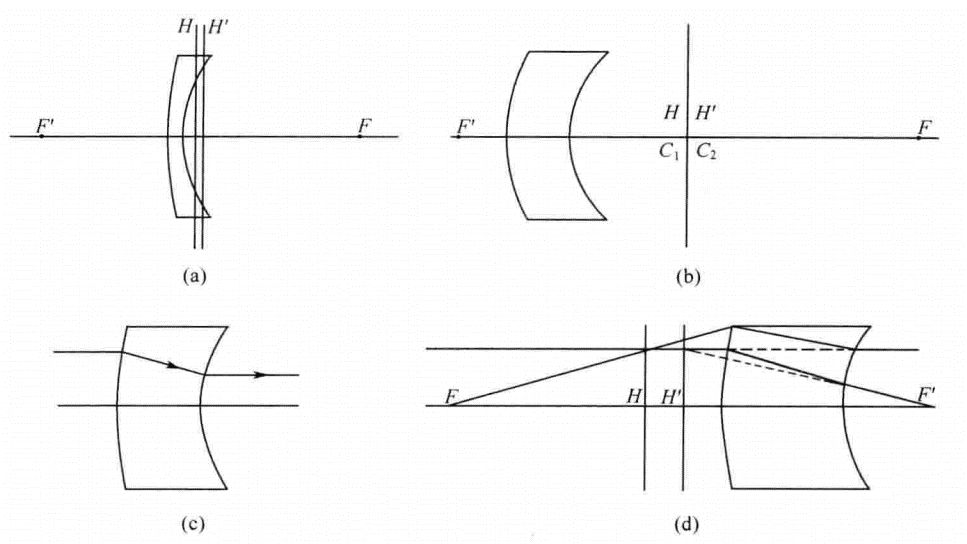
6. Meniscus concave lens
For this type of lens, the two surface curvature radius symbols are the same, but the absolute value of convex curvature radius is larger. It is similar to biconvex lens, and the positive and negative focal length changes with thickness. Because the radii on both sides of this lens are of the same number, the difference between the two radii is very small, and the effect of given positive power can be obtained without a large thickness. Therefore, the meniscus concave lens plays an important role in correcting the bending of the image plane.
End



