The imaging law of concave lens is: when the object is a real object, it becomes an upright and reduced virtual image, and the image and the object are on the same side of the lens. Concave lens has divergent effect on light, so the lens is also called divergent lens, negative spherical lens.
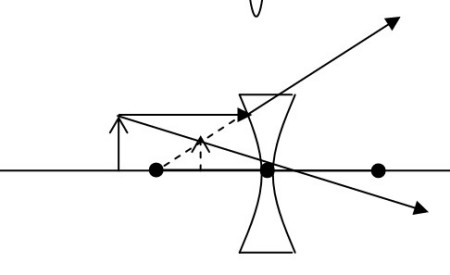
When the object is a real object, it becomes an upright and reduced virtual image.
When the object is virtual:
(since the focal length of the concave lens is negative and the object distance of the virtual object is also negative, the following focal length and object distance are taken as their absolute values)
When the object is a virtual object and the distance from the concave lens to the virtual object is within one focal length, it becomes an upright and enlarged real image, and the image and the object are on the same side of the lens; (u<f)
When the object is a virtual object and the distance from the concave lens to the virtual object is twice the focal length, the image is formed at infinity; (u=f)
When the object is a virtual object and the distance from the concave lens to the virtual object is beyond one focal length and within two focal lengths, it becomes an inverted and enlarged virtual image, and the image and the object are on the opposite side of the lens; (f<u<2f)
When the object is a virtual object and the distance from the concave lens to the virtual object is twice the focal length, it becomes an inverted, equal sized virtual image, and the image and the object are on the opposite side of the lens; (u=2f)
When the object is a virtual object and the distance from the concave lens to the virtual object is beyond twice the focal length, it becomes an inverted and reduced virtual image, and the image and the object are on the opposite side of the lens. (u>2f)
As the thickness increases, the situation becomes more complicated. When the thickness is large enough, it is equivalent to Galileo telescope, and when the thickness is larger, it will be equivalent to positive lens.
Image ipsilateral, V < u
The near image of an object becomes larger, and the far image of an object becomes smaller.
1 / U + 1 / F = 1 / V (U is the object distance, V is the image distance, f is the focal length, which is the same as that of convex lens). Note: u, F and V are positive numbers.
End



