To analyze which factors are related to the resolution of optical instruments, it is necessary to start with how optical instruments are imaged. The simple model is the “ideal lens” model. The “ideal lens” given solely from a geometric optical perspective does not matter in resolution, and no matter how close two points are, they can be clearly imaged separately. So let’s consider a bit more practical factors? Consider, for example, the volatility of light? Consider, for example, the aberration of the instrument? Okay, let’s start with these two paths separately.
When considering the fluctuation of light, it is necessary to consider the diffraction effect [1]. The following reference [1] provides an expression for calculating the light intensity distribution of circular aperture diffraction (i.e., Airy disk), and the specific calculation process is not complicated. In other words, if volatility is to be considered, an ideal point light source, even after passing through an ideal lens, cannot become a point image, but rather an Airy spot. This poses a resolution issue. If the two point sources are too close together, and the two Airy spots overlap each other after imaging, so that they appear to be a fuzzy halo, then the two point sources cannot be distinguished. Based on the Rayleigh criterion [2], it is believed that if the center of one Airy spot is located at the dark ring of the other Airy spot, then the two Airy spots cannot be distinguished.
Thereby deriving the so-called “diffraction limit”:
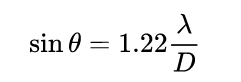
The theta angle above is the opening angle of the small resolvable point pair, the lambda on the right is the wavelength of the light, and D is the lens aperture. If it is a microscope, it is necessary to convert this angle to the corresponding distance on the object surface. The conclusion is similar, but instead of aperture D on the right, numerical aperture NA (related to aperture angle) is good. The above is for the fluctuation of light, so what effect does aberration have?
Aberration is another concept of geometric optics [3]. In simple terms, aberration makes the image formed by a point light source (from a geometric optical perspective) no longer a point, but a diffuse spot. This is somewhat similar to the diffraction effect of wave optics, but is essentially two completely different concepts. For example, the figure below demonstrates that the upper half of spherical aberration (a type of monochromatic aberration) is an ideal lens imaging, with parallel light strictly converging to a point; The lower part is a lens image with spherical aberration, and the parallel light cannot strictly converge to a point. Good quality instruments can correct various aberrations, but no matter how they are corrected, actual optical systems will have aberrations. In summary, the fluctuation of light and the aberration of the instrument itself cause the instrument to no longer have a point image of a point light source, leading to the concept of “resolution”. The aperture (angle) and working wavelength of an instrument affect resolution from the perspective of light fluctuation, while the aberration of the instrument affects resolution from the perspective of aberration in geometric optics. Due to the existence of chromatic aberration, the range of working wavelength of the instrument also affects the resolution of the instrument. In general, the resolution shown in Equation (1) above can be used as the resolution limit for an “ideal system” with infinitely small aberrations. In practical applications, some optical systems (such as telescope systems) have very small aberrations, and Equation (1) can be directly applied to estimate resolution.



